문제 설명
문제 출처: https://programmers.co.kr/learn/courses/30/lessons/67258
- 각각의 보석상은 하나의 보석을 판매
- 연속된 보석상들을 쇼핑하면서 방문할 때마다 보석을 구매
- 모든 종류의 보석을 구매할 때까지 진행
- 모든 종류의 보석을 구매하는 경우 중 가장 조금의 보석을 가장 앞선 보석상에서 구매하는 경우를 구하기
문제 접근
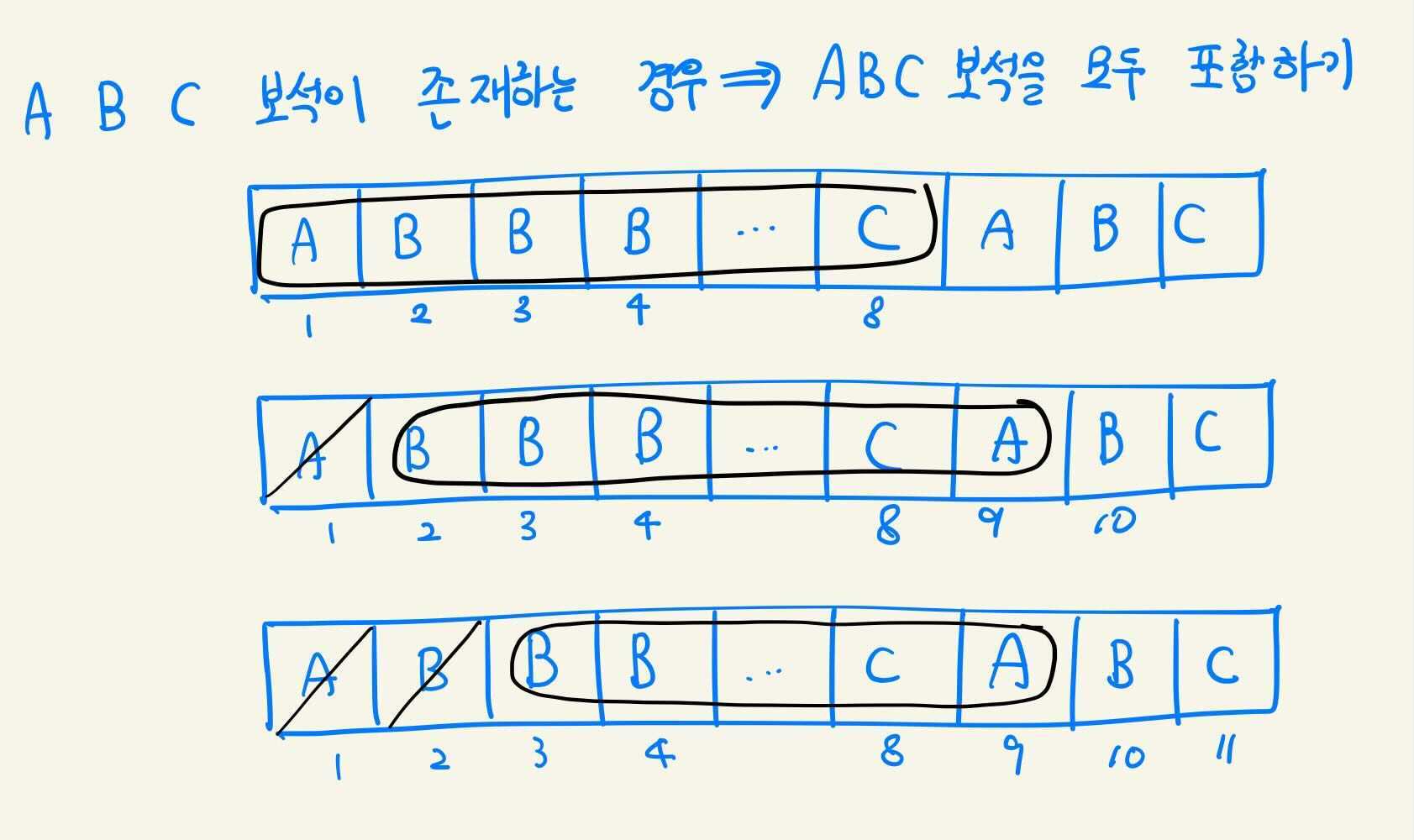
우선 단순하게 문제의 조건을 그림으로 나타내면 위와 같다. 결국 1번 상점부터 방문하는 경우, 2번 상점부터 방문하는 경우, … 이런 식으로 진행해나간 뒤 가장 보석을 적게, 앞의 상점에서 사는 경우를 구하면 된다.
👎 첫 번째 접근
‘‘각 경우마다 직접 구해볼까?’
허걱.. 보석상은 최대 10만개를 입력으로 준다. 각 경우를 매번 직접 N번 상점부터 시작해서 모든 종류의 보석을 사는 경우를 구하는 것은 너무 비효율적일 것 같다.
👍 두 번째 접근
“그러고보니 앞의 경우와 비교하면서 방금 제외된 보석만 추가되는 경우를 참고하며 구하면 되지 않을까?”
즉 그림을 보면 두 번째 경우는 앞의 경우(첫 번째 경우)와 비교했을 때 A가 줄었고, 내가 방문한 보석상 중 A가 없다면 A를 구매할 때까지 보석상을 방문하면 된다. 세 번째 경우는 그와 반대로 앞의 경우(두 번째 경우)와 비교했을 때 B가 줄었지만 내가 방문한 보석상 중 B를 판매하는 곳이 있기에 새로운 보석상을 방문할 필요가 없다.
=> 오호라… 추상적으로 접근 방식을 바라봤을 때는 효율적인 것 같다! 이제 구현에서만 잘 구현하면 되겠다.
구현
👍 올바른 구현
# 풀이법이 떠오르지 않는다. 처음 보는 유형이다...
# 그냥 1번에서 시작해서 다 포함하는 경우
# 2번에서 시작해서 다 포함하는 경우 이렇게 다 세보면 효율성이 오바일까..? 최대 10만칸임...
# 약간 dp스럽게 전꺼를 바탕으로 생각하는 게 좋겠다.
# 전꺼를 없앤 대신 걔가 포함되어있으면 ㄱㅊ은 거니까.
def solution(gems):
end = -1
gems_set = set(gems)
shopping_bag={}
for gem in gems_set:
shopping_bag[gem] = 0
for i in range(len(gems)):
gem = gems[i]
gems_set.discard(gem)
shopping_bag[gem] += 1
if len(gems_set) == 0:
end = i
break
answers = [(end+1, 0, end)]
for i in range(1, len(gems)):
found, end = shop(gems, i, end, shopping_bag)
if not found:
break
length = end - i + 1
if length == answers[0][0]:
answers.append((length, i, end))
elif length < answers[0][0]:
answers = [(length, i, end)]
# print(answers)
answer = sorted(answers)[0]
return [answer[1] + 1, answer[2] + 1]
# end 포함
def shop(gems, start, end, shopping_bag):
left_gem = gems[start-1]
is_complete = False
new_end = -1
shopping_bag[left_gem] -= 1
if shopping_bag[left_gem] == 0:
for i in range(end+1, len(gems)):
shopping_bag[gems[i]] += 1
# 이전에 뺸 녀석을 찾은 경우
if gems[i] == left_gem:
is_complete = True
new_end = i
break
else:
is_complete = True
new_end = end
return is_complete, new_end
내가 방문하면서 구매한 보석들의 각각의 개수를 딕셔너리를 통해 관리했다.
이전 시도 때 구매한 보석들의 각각의 개수를 참고해 만약 이전에 1번 보석상에서 A 보석을 구매하는 것을 시작으로 했다면 이번 시도에는 2번 보석상에서 어떤 보석을 구매하게 될 것이다. 이 경우 이젠 1번 보석상에서 A 보석을 구매할 일이 없으니 딕셔너리에서 A 보석의 개수를 1개 줄여주고 시작을 하는 것이다. 이후 구매 개수가 0개가 되는 보석이 없는지 확인하고 존재한다면 해당 보석을 구매할 때까지 계속해서 보석상을 방문해나가면 된다.
- 보석의 모든 종류를 구하기 위해서는 Set 자료 구조를 이용했다.
- 구매한 보석을 순서대로 리스트로 관리하며 리스트에 내가 구매한 보석이 있는지 찾는 방식은
__contains__를 이용하게 되고 이 작업만 놓고 보면 시간 복잡도가 O(n)이다. 반면 딕셔너리에 각 보석의 구매 개수를 이용해 구매하지 않은 보석이 있는지 확인하는 작업은 O(1)이다. 따라서 딕셔너리를 이용해 보석을 구매했는지를 확인하는 방식을 이용했다.
👎 실패했던 구현
이 부분은 개인적으로 기억하려는 의도로 작성한 것이기 때문에 설명이 이상할 수 있습니다.
- list를 이용해 내가 구매한 보석을 순서대로 담았던 방식
위에서도 언급은 했지만 list를 이용해 내가 구매한 보석을 순서대로 담은 뒤 어떤 보석을 적어도 한 번 구매한 적이 있는지를 in 으로 찾는 방식을 이용한 경우이다. 게다가 이전 시도에서 left_gem을 제거한 뒤 새로운 shopping_bag을 대입하는 과정에서 아래와 같이 O(n)의 복잡도를 갖는 list slicing을 이용하다보니 더욱 비효율적이었다. 프로그래머스의 효율성 테스트를 5개 실패했다.
shopping_bag = shopping_bag[1:]
- 1번 방식을 개선해 list slicing이 아닌 dequeue 자료구조 이용하기
list slicing 시 O(n)의 시간 복잡도를 갖는 list가 아닌 앞의 요소를 제거하면서도 O(1)의 시간 복잡도를 갖는 dequeue 자료구조를 이용했다. 하지만 프로그래머스 효율성 테스트를 2개 실패했다.
즉 요점은 list든 dequeue든 둘 중 무엇을 이용하더라도 O(n)의 시간 복잡도를 갖는 in을 통해 특정 요소가 collection 내에 존재하는 것이 비효율적이므로 딕셔너리를 이용해 O(1)의 시간 복잡도를 갖는 방식을 이용하는 것이다.